時系列の学習には、リカレントニューラルネットワーク(RNN)を使います。その一つに、Long short-term memory (LSTM)という記憶セルを使うやり方があります。その実装についての忘備録です。
ネットワークとやりたいこと
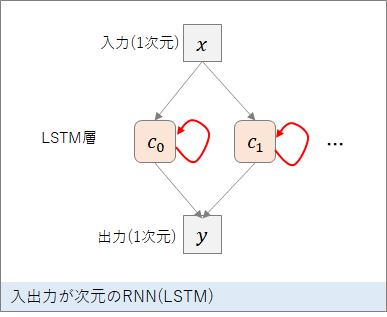
入出力が1次元で中間層に20個のLSTMユニットを使ったシンプルなネットワークを考えます。x(t)を入力するとy(t)を出力しますが、LSTMユニットがあるので、y(t)は、過去から今までの入力 x(0), x(1), …, x(t-1), x(t) に依存した値となります。
具体的な応用として、時系列信号の予測があります。
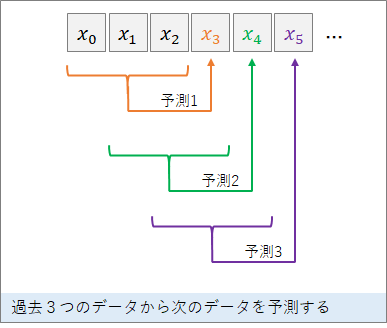
多くのブログや本で紹介されているのは、以下のように、入力を複数ステップ入れて次の信号を予測する、それを毎回繰り返す、というものです。
しかし、このような予測方法でしたら、LSTMを使わなくても、通常の他入力1出力のニューラルネットワークモデルで、過去の複数の信号値と次の信号値の対応を学習することで予測が可能です。
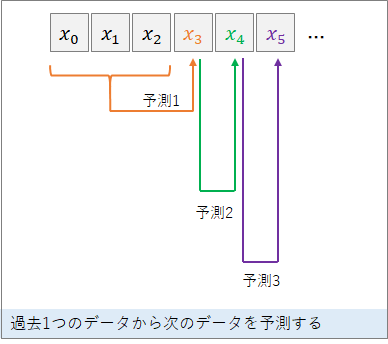
そこで、以下のように、初めだけ複数の入力を入れたら、1つの入力に対して1つの予測を次々に行うようなLSTMを試してみました。
データ
RNNの場合、データをどう作るかが結構ややこしいですね。高速化や安定化のためには、バッチを想定すべきですが、それも時系列の順番が正しくなるように気を付ける必要があります。
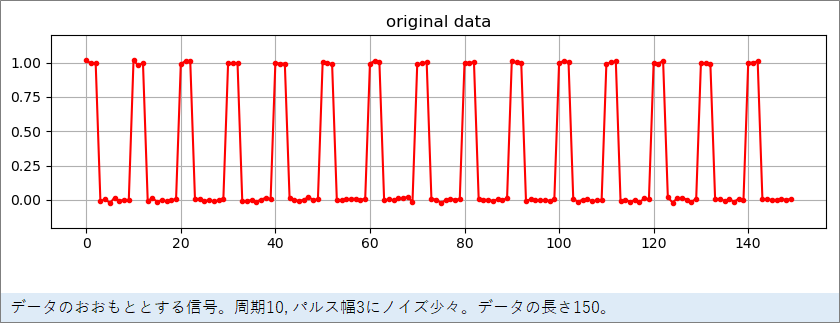
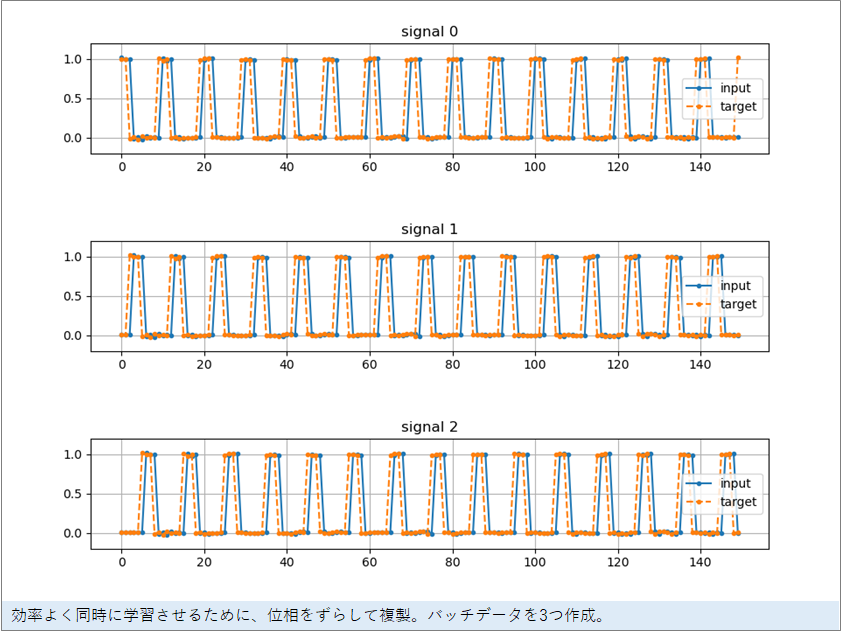
まず、sin波よりも予測が難しいと思われる以下のような周期10のパルス波のデータを作りました。150個のデータです。このような信号だと、次のパルスのタイミングを正確に予測をするためには、内部で数を数える仕組みが必ず必要になります。
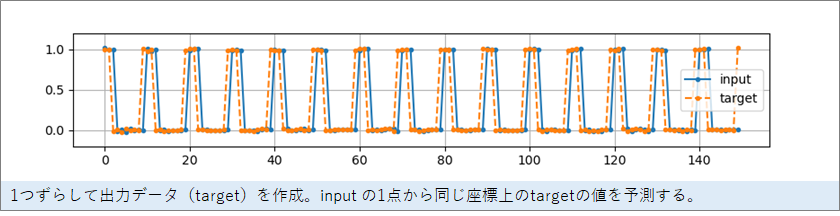
このデータから次の信号を予測するので、出力の目標とする信号(ターゲット信号)は、点線のようになります。
さて、複数の時系列を同時に学習させた方が学習の効率や安定性が良いので、位相をずらした3つの信号を作成します(本来なら信号の数はもっと増やした方がよいと思いますが、図解で見やすいように3にしています)。
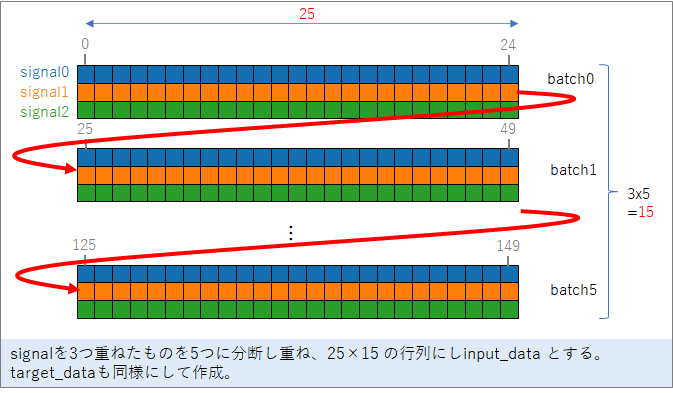
この3つの信号を、適当な長さ(ここでは25)で分断し重ねて、25 x 15 の行列にします。これが実際に使うinput_data となります。同様に、ターゲット信号からtaregt_data も作ります(input_data から、1ずれているだけです)。
実際にinput_data を図示すると下のようになります。

このinput_data とtarget_dataを生成するプログラム(make_data_pulse.py)は以下になります。引数をTrueにすると生成過程が図示されます。
import numpy as np
import matplotlib.pyplot as plt
signal_length = 150 # 信号の全データ 1epoch
period_length = 10 # 周期
pulse_dulation = 3 # パルス幅
data_length = 25 # 1バッチのデータの長さ
batch_size = 3 # バッチ数(まとめて学習させるデータ数)
batch_n = int(signal_length / data_length) # 1epoch中のバッチの数
def generate_data(f_show):
# 1周期分の信号の生成
p1 = [1 if i < pulse_dulation else 0 for i in range(period_length)]
# 信号の全データ生成
signal_all = np.zeros(signal_length)
for i in range(int(signal_length / period_length)):
signal_all[period_length*i:period_length*(i+1)] = p1
signal_all += 0.01 * np.random.randn(signal_length) # ノイズ加算
# 全データ表示
if f_show:
plt.figure(figsize=(10, 2.5))
plt.plot(signal_all, '.-r')
plt.ylim(-0.2, 1.2)
plt.grid(True)
plt.title('original data')
plt.show()
# 位相をずらして3つの信号を生成
dp = int(period_length / batch_size)
signals = np.zeros((batch_size, signal_length))
signals[0, :] = signal_all
for i in range(1, batch_size):
signals[i, dp*i:-1] = signal_all[:-(dp*i+1)]
signals[i, :dp*i] = signal_all[-dp*i:]
# 予測の教師データを生成
signals_next = np.zeros((batch_size, signal_length))
for i in range(batch_size):
signals_next[i, :-2] = signals[i, 1:-1]
signals_next[i, -1] = signals[i, 0]
if f_show:
plt.figure(figsize=(10, 7.5))
plt.subplots_adjust(hspace=0.8)
for i in range(batch_size):
plt.subplot(batch_size, 1, i + 1)
plt.plot(signals[i,:].T, '.-', label='input')
plt.plot(signals_next[i,:].T, '.--', label='target')
plt.ylim(-0.2, 1.2)
plt.legend()
plt.grid(True)
plt.title('signal %d' % i)
plt.show()
# データの長さ data_length で分割
input_data = np.zeros((batch_size * batch_n, data_length, 1))
target_data = np.zeros((batch_size * batch_n, data_length, 1))
id = 0
for i in range(batch_n): # 5
for j in range(batch_size): # 3
try:
input_data[id, :, 0] = signals[j, data_length*i:data_length*(i+1)]
target_data[id, :, 0] = signals_next[j, data_length*i:data_length*(i+1)]
id += 1
except Exception as e:
print(e)
pdb.set_trace()
if f_show:
plt.figure(figsize=(10, 7.5))
plt.subplots_adjust(hspace=0.8)
id = 0
for i in range(batch_n):
plt.subplot(batch_n, 1, i + 1)
for j in range(batch_size):
plt.plot(input_data[id, :, 0], '.-', label='id %d' % j)
id += 1
plt.ylim(-0.2, 1.2)
plt.grid(True)
# plt.legend()
plt.title('batch %d' % i)
plt.show()
return signal_all, input_data, target_data
if __name__ == '__main__':
signal_all, input_data, target_data = generate_data(f_show=True)
print('input_data ', input_data.shape)
print('target_data ', target_data.shape)
学習と予測
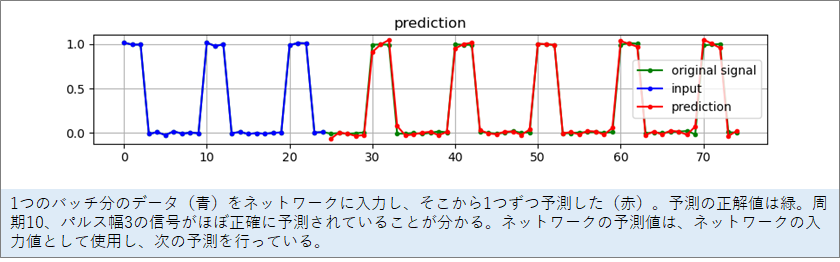
以上の学習データを使ってネットワークを学習させ予測させた結果です。
初めの25個の時系列(青)を逐次ネットワークに入力し、26個目の出力から赤でプロットしています。緑がオリジナルの信号で、赤が緑に重なると正しく予測できたことになります。
予測がうまくいっていることが分かります。
学習と予測のコードは以下に乗せました。ポイントは以下の2つです。
1.ネットワークの内部状態を出力するために、Sequenceモデルではなく、functional APIでモデルを構築している。
2.LSTM層の引数に、return_state=True(内部状態を出力する), return_seqnences=True(入力に対して逐次出力), stateful=True(バッチ間でも内部状態を保持する)を入れている。
学習はすぐに終わります。私の一昔前のノートPC(GPUなし)で23秒でした。
import numpy as np
import matplotlib.pyplot as plt
import time
from keras.layers import Input
from keras.models import Model
from keras.layers.core import Dense, Activation
from keras.layers.recurrent import LSTM
import make_data_pulse as mdp
np.random.seed(1)
# データ生成
signal_all, input_data, target_data = mdp.generate_data(f_show=False)
# f_show=True にすればデータのグラフが表示される
# -- ニューラルネットワーク --
net_in = 1 # 入力層のニューロン数
net_mid = 20 # 中間層のニューロン数
net_out = 1 # 出力層のニューロン数
epochs = 400
# モデル構築
inputs = Input(
shape=(None, net_in),
batch_shape=(mdp.batch_size, None, net_in)
)
xx, state_h, state_c = LSTM(units=net_mid,
return_state=True, # 内部状態を出力
return_sequences=True, # 逐次出力
stateful=True # バッチ間の状態維持
)(inputs)
predictions = Dense(net_out, activation='linear')(xx)
model = Model(inputs=[inputs], outputs=[predictions, state_h, state_c])
# 学習
stime = time.time()
model.compile(
optimizer="rmsprop",
loss={'dense_1': 'mean_squared_error'}
)
model.fit(
{'input_1': input_data},
{'dense_1': target_data},
batch_size=mdp.batch_size,
epochs=epochs,
verbose=1,
shuffle=False
)
print('time %.2f sec' % (time.time() - stime))
# 入力1バッチ分
model.reset_states()
xx, hh, cc = model.predict(input_data[:mdp.batch_size, :, :])
# 1データずつ予測
prediction = []
n_predict = 50
ccs = []
hhs = []
for i in range(n_predict):
prediction.append((xx[0, -1, 0]))
ccs.append(cc[0, :])
hhs.append(hh[0, :])
xx, hh, cc = model.predict(xx[:, -1, 0].reshape(mdp.batch_size, -1, 1))
# グラフ表示
plt.figure(figsize=(10, 7.5))
plt.subplot(3,1,1)
plt.subplots_adjust(hspace=0.8)
plt.plot(signal_all[:mdp.data_length+n_predict], '.-g', label='original signal')
plt.plot(range(mdp.data_length), input_data[0, :, 0], '.-b', label='input')
plt.plot(
range(mdp.data_length, mdp.data_length + n_predict),
prediction,
'.-r',
label='prediction',
)
plt.grid(True)
plt.legend()
plt.title('prediction')
plt.subplot(3,1,2)
plt.plot(0, 0)
plt.plot(range(mdp.data_length, mdp.data_length + n_predict), ccs)
plt.grid(True)
plt.title('c')
plt.subplot(3,1,3)
plt.plot(0, 0)
plt.plot(range(mdp.data_length, mdp.data_length + n_predict), hhs)
plt.grid(True)
plt.title('h')
plt.show()
中間層
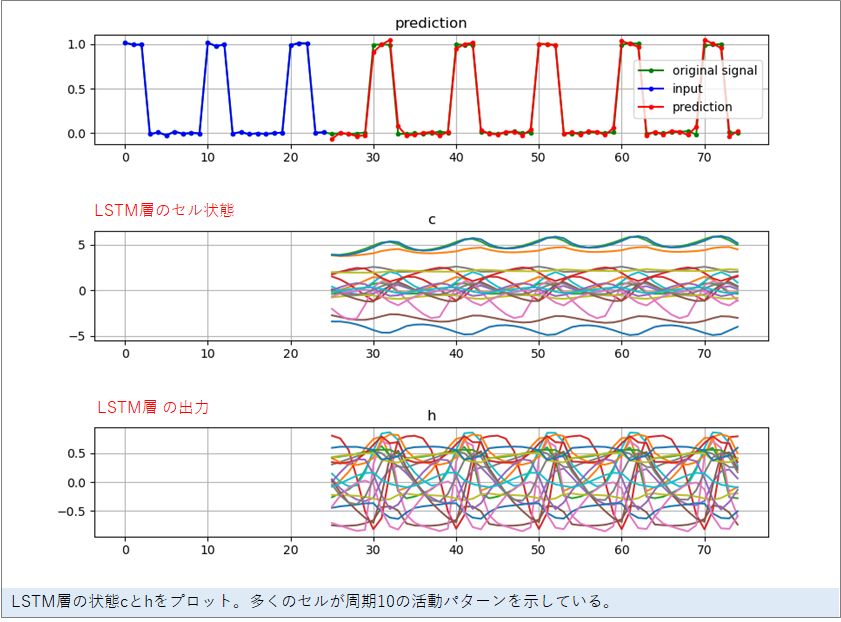
さて、LSTMのメモリーによって、0の回数を数えるメカニズムが生成されているはずです。LSTMのメモリーセル(c)、そして、LSTMの出力(h) はどのような値をとっているのでしょう。それも出力されるように作りました。
内部を見てみると、0を出力しているあいだでも、セルの活動は周期10で変化し続けていることが分かります。複数のセルが入れ替わり立ち代わり活動を上げることで数を数えているようです。
動物に数を数えさえるタスクを覚えさせて脳活動を測定したら、このような記録がとれるのではないでしょうか。興味深いですね。