はじめに
ライフゲームを「画像処理の2次元フィルタ」で高速化できるのでは?と思いついて、openCVの`filter2D`という関数で試してみました。
その結果、うまく実装することができまして、20倍以上も早くなりました。2重のforループの処理が、2次元フィルタの処理1回に置き換えられるところがポイントです。これだけ早くなると全然違うものに見えます。テンション上がりますね!この方法は、ライフゲームだけでなく、いろいろなセルオートマトンの実装に応用できると思います。
この記事のプログラムコードは、windows10, python3.6, OpenCV3.4 の環境で試したものです。
全コードはgithub -> [こちら]
ライフゲームを、画像処理用の2Dフィルターで22倍に加速させる。python3, openCV3 pic.twitter.com/11x7xEtie3
— いとしん (@makocchinote) 2019年3月21日
ライフゲームとは
ライフゲームとは、2次元の盤上で生物が生まれたり死んだりするバターンを眺める、凄く奥の深いシミュレーションです。詳しくは -> [こちら]
ルールは以下の二つのみです。
1. 生物の周り8セルに、2匹または3匹の他の生物がいると、次の世代もその生物は生きる。そうでなければ死ぬ。
2. 生物がいないセルでは、周り8セルに3匹の生物がいると、新しく生物が生まれる。
このルールですべてのセルを更新して1世代とし、何世代も繰り返しながら、生物の分布パターンを観察するのがライフゲームです。
周囲のセルを数える
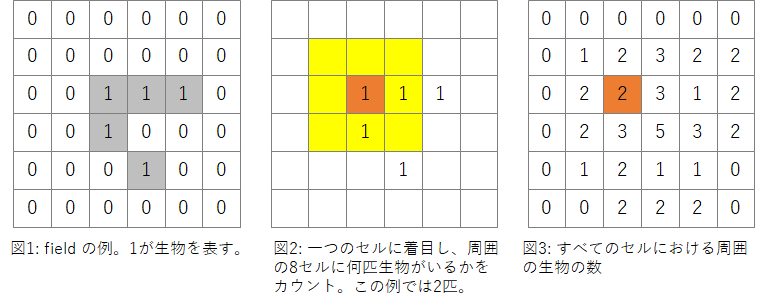
そういうことで、ライフゲームを動かすには、「すべてのセルについて周囲の8セルの生物の数を数える」という処理がキモになります(図1-3)。生物がいるところを1とし、いないところを0とします。
プログラムするために、まず、各セルに生物がいるかいないかを記述する2次元配列`field`を定義しましょう。
field = np.array([[0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0],
[0, 0, 1, 1, 1, 0],
[0, 0, 1, 0, 0, 0],
[0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 0, 0]], dtype=np.uint8)
「すべてのセルについて周囲の8セルの生物の数を数える」処理をpythonで普通に書くと2重のforループで以下のようになると思います(端のセルの処理は省略しています)。
count = np.zeros()count = np.zeros((6, 6), dtype=np.uint8)
for i in range(1, 5):
for j in range(1, 5):
count[i, j] = field[i-1,j-1]+field[i-1,j]+field[i-1,j+1] \
+ field[i ,j-1] +field[i ,j+1] \
+ field[i+1,j-1]+field[i+1,j]+field[i+1,j+1]
ところで、画像処理の手法の1つに、**2Dフィルター**というものがあります(図4)。2Dフィルターでは、カーネルと呼ばれる2次元行列を定義します。カーネルと「同じ大きさの入力画像の小領域」との内積を計算し、その値を出力値とします。この処理をすべての画素に対して行い出力画像を得ます。
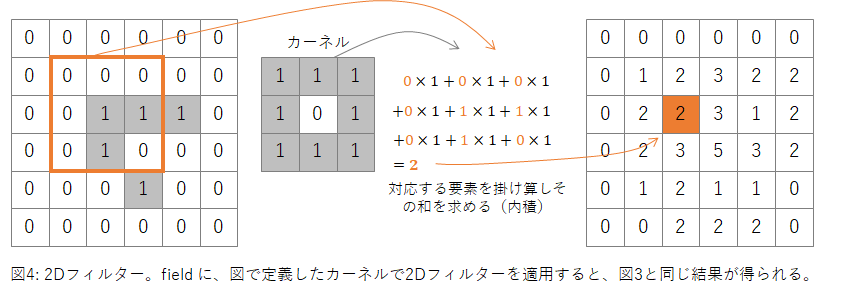
カーネルを変えることで、エッジを強調したり、全体をぼやかしたりなどと、いろいろな効果を得ることができるのですが、図4に示したようなドーナッツ状のカーネルを使うと、セルの周囲の1を数えるという、図3で示したものと同じ効果を得ることができます。
コードでは、`openCV` の`filter2D`を使って以下のように簡単に実装できます。
kernel = np.array([[1,1,1],[1,0,1],[1,1,1]], dtype=np.uint8) count = cv2.filter2D(field, -1, kernel) print(count)
出力のcount の中身は以下のようになり、図3と同じ結果が得られたことが分かります。
[out] count= [[0 0 0 0 0 0] [0 1 2 3 2 2] [0 2 2 3 1 2] [0 2 3 5 3 2] [0 1 2 1 1 0] [0 0 2 2 2 0]]
残りの処理もfor文やif文を使わずに実装
さて、filter を使って`count`が得られましたが、もう少しやることがあります。
ライフゲームのルール1と2から、
1. `field[i, j] = 1` となる`i, j`について、 `count[i, j]=2 or 3`だったら、次の世代で、`field_next[i, j] = 1` とする
2. `field[i, j] = 0` となる`i, j`について、 `count[i, j]=3`だったら、次の世代で、`field_next[i, j] = 1` とする
の計算をしなくてはいけません。そしてここでも forループなしでコードを書きたいところです。
ところで、行列に論理演算子を適用すると、その結果はbool型の行列が帰ってきます。
print(count == 2)
とすると、
[out]
array([[False, False, False, False, False, False],
[False, False, True, False, True, True],
[False, True, True, False, False, True],
[False, True, False, False, False, True],
[False, False, True, False, False, False],
[False, False, True, True, True, False]])
と出力されます。この性質を使って1と2を計算することはできないでしょうか。ちなみに、結果に1をかけると0/1 で表示されて見やすくなります。
print((count==2)*1) [out] [[0 0 0 0 0 0] [0 0 1 0 1 1] [0 1 1 0 0 1] [0 1 0 0 0 1] [0 0 1 0 0 0] [0 0 1 1 1 0]]
`行列[count == 2] = 9` などとすることで、`True`に対応する要素を`9`に書き換えることができます。
tmp = np.zeros((6, 6), dtype=np.uint8) tmp[(count==2)] = 9 print(tmp) [out] [[0 0 0 0 0 0] [0 0 9 0 9 9] [0 9 9 0 0 9] [0 9 0 0 0 9] [0 0 9 0 0 0] [0 0 9 9 9 0]]
行列同士の論理演算は、例えば、’A and B’ などができるような気がするのですが、これだとエラーになってしまいます。ここは ‘A * B’ とするとうまくいきます。’A or B’ は ‘A + B’ でできます(このあたりいろいろ試してたどり着きましたが、もっと良い方法がありましたら教えてください)。
A = np.array([False, False, True, True])
B = np.array([False, True , False, True])
print('A=', A*1, ', B=', B*1)
print('A and B =', (A * B)*1)
print('A or B =', (A + B)*1)
[out]
A= [0 0 1 1] , B= [0 1 0 1]
A and B = [0 0 0 1]
A or B = [0 1 1 1]
さて以上の性質を使うと、
「`field = 1` で、 `count = 2 or 3`である」となるbool の行列 (`alive`)と、
「`field = 0` で、 `count = 3`である」となるbool の行列 (`born`)を
以下のように求めることができます。
alive = (field == 1) * ((count == 2) + (count == 3))
born = (field == 0) * (count == 3)
print('alive=')
print(alive * 1)
print('born=')
print(born * 1)
[out]
alive=
[[0 0 0 0 0 0]
[0 0 0 0 0 0]
[0 0 1 1 0 0]
[0 0 1 0 0 0]
[0 0 0 0 0 0]
[0 0 0 0 0 0]]
born=
[[0 0 0 0 0 0]
[0 0 0 1 0 0]
[0 0 0 0 0 0]
[0 0 0 0 1 0]
[0 0 0 0 0 0]
[0 0 0 0 0 0]]
よって次世代のfield(`field_next`)は以下のように求めることができます。
field_next = np.zeros_like(field, dtype=np.uint8)
field_next[np.where(alive)] = 1
field_next[np.where(born)] = 1
print('field_next=')
print(field_next)
[out]
field_next=
[[0 0 0 0 0 0]
[0 0 0 1 0 0]
[0 0 1 1 0 0]
[0 0 1 0 1 0]
[0 0 0 0 0 0]
[0 0 0 0 0 0]]
# まとめ
以上をまとめると、以下のようになります。
field = np.array([[0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0],
[0, 0, 1, 1, 1, 0],
[0, 0, 1, 0, 0, 0],
[0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 0, 0]], dtype=np.uint8)
kernel = np.array([[1,1,1],[1,0,1],[1,1,1]], dtype=np.uint8)
count = cv2.filter2D(field, -1, kernel)
alive = (field == 1) * ((count == 2) + (count == 3))
born = (field == 0) * (count == 3)
field_next = np.zeros_like(field, dtype=np.uint8)
field_next[np.where(alive)] = 1
field_next[np.where(born)] = 1
print('field=')
print(field)
print('field_next=')
print(field_next)
[out]
field=
[[0 0 0 0 0 0]
[0 0 0 0 0 0]
[0 0 1 1 1 0]
[0 0 1 0 0 0]
[0 0 0 1 0 0]
[0 0 0 0 0 0]]
field_next=
[[0 0 0 0 0 0]
[0 0 0 1 0 0]
[0 0 1 1 0 0]
[0 0 1 0 1 0]
[0 0 0 0 0 0]
[0 0 0 0 0 0]]
これで、lifegame の世代交代をfor ループなしで実装できます!この方法を、「フィルター法」とでも名付けましょう。
実際に作ったコードは[github]にUPしてあります。
ここでは、
+ 上下左右をつなげる周期境界条件
+ fps の計算表示
+ 従来法とフィルター法の切り替え(space key)
の機能も追加してあります。従来法に比べてフィルター法は、僕のPCだと22倍早くなりました(field のサイズや表示の仕方にもよります)。気持ちいいです!
この方法は、ライフゲームに限ったものではなく、他のセルオートマトンなどにも使えると思います。